ОБЩИЙ МЕТОД РАСЧЕТА ДОЗ ФЛИКЕРА НАПРЯЖЕНИЯ

Э.Г. Куренный, Е.Н. Дмитриева, Н.В. Цыганкова, Л.В. Черникова

Донецкий государственный технический университет

ул. Артема, 58, Донецк-00, 83000, Украина

Тел. +38 (062)335-42-76, E-mail: led@donntu.ru

Annotation – The task of estimation of electromagnetic compatibility (EMC) by flicker dose by calculation way is considered. Flicker model IEC is used. The analytic method of dose flicker calculation, which is based on weighting filter in the form of connected in parallel linear inertial links is proposed.

Key words – EMC, flicker model, flicker dose, vision reaction, flicker sense, calculation methods.

Постановка задачи. Колебания напряжения в осветительных электрических сетях вызывают дополнительное утомление человека, ухудшая его зрение и уменьшая производительность труда. Универсальным объективным показателем допустимости колебаний есть доза фликера PST напряжения [1 – 3]. В действующих электрических сетях доза измеряется фликерметром, а в проектировании – расчетным путем. В [1] рекомендуются приближенные методы расчета лишь для частных случаев детерминированных колебаний прямоугольной и треугольной формы – к тому же с существенными ограничениями интервалов времени между соседними колебаниями. Разработка общего метода без ограничения по виду колебаний является целью статьи.

Идентичность результатов расчета любого показателя электромагнитной совместимости (ЭМС) обеспечивается, если измерительный прибор и методы расчета используют единую математическую модель ЭМС. Для определенности далее рассматривается принятая в [2] и [3] математическая фликер-модель системы лампа –

глаз – мозг.

Исходными данными являются реализации (графики) процессов U(t) изменения во времени t действующих значений напряжения или их характеристики. Будем рассматривать периодические, детерминированные непериодические и стационарные случайные процессы. В последнем случае задаются корреляционные функции (КФ) K(t ). Обобщение результатов на нестационарные случайные процессы не вызывает затруднений.

Математическая модель. Фликер-модель состоит из трех блоков: входного БВ, взвешивающего фильтра ФВ, квадратичного инерционного сглаживания КС и статистической обработки ОС (рис.1). Первый блок выделяет помеху ЭМС X(t): разность между процессом U(t) и его одноминутным трендом. Помеха измеряется в процентах от уровня номинального напряжения Uн.

Рис. 1. Структурная схема фликер-модели

Второй блок моделирует лампу накаливания (60 Вт, 230 В) и зрительную систему человека. Он включает в себя три линейных фильтра: 1 – верхних частот с частотой среза 0,05 Гц, 2 – Баттерворта шестого порядка с частотой среза 35 Гц и 3 – фильтр восприятия. С учетом данных [2 – 4] передаточные функции фильтров запишем в виде:

, (1)

, (2)

 

, (3)

где – коэффициент передачи; с, с, с,

с, , , , ,

, – постоянные времени, р – оператор дифференцирования.

Передаточная функция взвешивающего фильтра

. (4)

Частота колебаний в [1] измеряется в мин –1, что соответствует частоте изменения процесса в Гц или угловой частоте в с–1. На рис. 2 приведены амплитудно-частотные характеристики (АЧХ) А(l ): 1 – взвешивающего фильтра и 2 – фильтра восприятия.

Рис. 2. Амплитудно-частотные характеристики фильтров

Процесс Y(t) на выходе ФВ назовем реакцией зрения, которая измеряется в процентах. Блок КС моделирует ощущение фликера S(t). Блок состоит из квадратора 4 и апериодического инерционного звена 5 первого порядка, которое сглаживает процесс Z(t)=Y 2(t) с постоянной времени и коэффициентом передачи , который делает величину S безразмерной (см. Приложение).

В последнем блоке на графике S(t) проводятся различные уровни фликера Pr и строится функция Er(Pr) кумулятивных вероятностей Er, выражаемых в процентах. Вероятность связана с функцией распределения F(S) ощущений фликера соотношением

.

По значениям Er = 0,1; 1; 3; 10 и 50 % находятся соответствующие уровни фликера . Доза фликера (в [2] – уровень резкости фликера) определяется по формуле

. (5)

Допустимое значение дозы равно единице.

Фликер-модель содержит линейную и нелинейную части, в связи с чем решение задачи производится в два этапа: вначале находятся характеристики реакции зрения после взвешивающего фильтра, а затем – зрительного ощущения. На первом этапе корректно применение принципа суперпозиции, что не только упрощает решение по предлагаемому далее методу, но и позволяет получать решение при наличии группы электроприемников с резкопеременной нагрузкой.

Метод парциальных реакций. Как видно из (1) – (4), взвешивающий фильтр описывается линейным дифференциальным уравнением 11 порядка, что существенно затрудняет применение общих формул теории автоматического управления: даже для определения переходной функции h(t). В связи с этим для решения используем метод парциальных реакций [5], согласно которому взвешивающий фильтр представим в виде параллельно включённых инерционных звеньев первого порядка с коэффициентами передачи a1,…,a11 и постоянными времени J1 , …, J11. Тогда вместо (4) получим

где , – корни (полюса) знаменателя передаточной функции.

Результаты расчета параметров звеньев по формулам (7) – (9) из [5] для краткости здесь не приводятся. Восемь звеньев из 11 имеют комплексные параметры, но в конечных выражениях мнимые величины отсутствуют.

Переходная функция взвешивающего фильтра получается суммированием парциальных переходных функций инерционных звеньев:

, (6)

где . График этой функции представлен на рис. 3 (кривая 1), где для сравнения показана переходная характеристика фильтра восприятия (кривая 2).

При воздействии помехи X(t) на выходе i-го инерционного звена наблюдается парциальная реакция . Искомая реакция

. (7)

 

Рис. 3. Переходные характеристики фильтров

Детерминированные реакции. Согласно [1] непериодические помехи должны задаваться в пределах каждых двух часов в течение суток. Записанный график помехи разбивается на m участков. На ν-ом участке помеха задается в виде некоторой функции . В проектных расчетах и в [1] используется кусочно-линейное представление помехи, когда , где – начальная ордината, а – угловой коэффициент.

Вычитание из помехи постоянной величины не изменяет вида реакции, что позволяет подобрать удобный для вычислений график помехи. Например, колебания напряжения прямоугольной формы в пределах от Umin до Umax вычитанием величины Umin представляются в виде последовательности прямоугольных импульсов величиной Umax – Umin и нулевых пауз.

При наличии нескольких электроприемников с резкопеременными нагрузками помеха получается суммированием помех от каждого электроприемника.

Для каждого участка, начиная с первого, по формуле общего решения дифференциального уравнения первого порядка, т.е. для каждого инерционного звена, определяются парциальные реакции

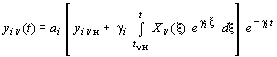, (8)

где x – переменная интегрирования, – ордината реакции в начале участка. На первом участке начальная ордината равна нулю, на втором – равна ординате в конце первого участка и т.д. Для кусочно-линейных помех

, (9)

где – длительность ν-го участка.

Перейдем к периодическим помехам, которые достаточно рассмотреть в пределах длительности цикла tц. Решение целесообразно находить последовательно, начиная с первого цикла, для которого согласно (8) при

.

Для определения начальной ординаты реакции в [6] была введена обобщенная весовая функция

,

которая позволяет найти частное решение дифференциального уравнения первого порядка

, (10)

зависящее от вида функций на всех участках.

Так как слагаемое с интегралом в (8) представляет собой общее решение дифференциального уравнения, то частное решение можно представить в виде

,

откуда найдем начальную ординату

, (11)

чем согласно (8) определяется парциальная реакция на первом участке. Ее конечная ордината, равная , является начальной для второго участка, что позволяет по той же формуле (8) найти реакцию на этом участке, и т.д. Контроль правильности решения выполняется по конечной ординате реакции при , которая должна совпадать с (11), а также по среднему значению реакции, равном нулю.

Для используемых в проектировании кусочно-линейных помех формулы (9) и (10) дают решение в конечном виде: на первом участке в принужденном режиме

, (12)

где

. (13)

Здесь при ν = 1 , ; при ν =2 .

В [1] области применимости приближенных методов расчета колебаний напряжения разграничиваются по длительности интервала между соседними размахами: больше или меньше 1 с, поскольку это значение является временем затухания переходной функции взвешивающего фильтра. Расчет по формуле (6) показывает, что за 1 с переходная функция входит в интервал ± 1,25 % от ее максимума, равного 56 %. Если помеха содержит участки с неизменными ординатами длительностью более 1 с, то в конце этих участков реакция практически равна нулю, что упрощает расчеты.

Объем вычислений можно сократить в зависимости от расположения спектра Фурье помехи относительно полосы пропускания взвешивающего фильтра. Если спектр захватывает только правую часть диапазона (0,05; 35) Гц, то блок 1 не влияет на результат, а в (6) и (7) останется по 10 слагаемых. Если захватывается левая часть, то блок 2 не изменяет вида реакции, а в формулах остается 5 слагаемых. Если же спектр находится внутри диапазона, то остается лишь фильтр восприятия и 4 слагаемых (например, в [5] ).

Случайные реакции. При случайных помехах решение может быть найдено методами имитации или аналитически. В первом случае имитируется ансамбль реализаций случайных помех (например, [7] ), каждая из которых представляет собой детерминированную непериодическую функцию. Применением к реализациям формулы (8) получается искомый ансамбль реакций. Во втором случае необходимо найти КФ реакции.

На входы инерционных звеньев поступает одна и та же помеха, поэтому парциальные реакции в (7) оказываются коррелированными. По этой причине для решения требуется найти не только КФ k(t ) парциальных реакций, но и взаимные КФ kir(t ) между попарно взятыми i-ой и r-ой реакциями. Соответствующие общие формулы теории вероятностей (например, (6.6.10) и (6.10.2) в [8] ) представим в виде (при t ³ 0):

, (14)

 

. (15)

Искомую КФ определим по формуле для КФ суммы коррелированных случайных процессов:

. (16)

Количество слагаемых в формуле (16) . Как и для периодических помех, оно может быть уменьшено. Если спектральная плотность помехи захватывает правую часть диапазона (0,05; 35), то остается 10 звеньев, поэтому вместо 121 будет 100 слагаемых. При захвате слева будет 5 звеньев и 25 слагаемых, а при нахождении внутри полосы пропускания – 4 звена и всего 16 слагаемых.

Несмотря на большое количество слагаемых, по сравнению с расчетами с использованием исходной передаточной функции (4) применение метода парциальных реакций дает существенное упрощение вычислений, так как для встречающихся на практике КФ интегрирование по формулам (14) и (15) выполняется в конечном виде и только один раз – разработчиками метода. Пользователю достаточно задать лишь параметры КФ. Например, для экспоненциально-косинусоидальной КФ

со стандартом s и параметрами a , w 0 при a ¹ g получим следующие выражения:

, (17)

 

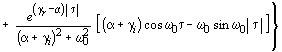. (18)

Характеристики ощущения фликера. Нелинейность блока КС исключает возможность раздельного рассмотрения парциальных реакций, поэтому при анализе ощущения фликера используется реакция (7). В случае детерминированных непериодических помех эта реакция возводится в квадрат, а процесс

подвергается инерционному сглаживанию. Аналогично (8) при нулевых начальных условиях ощущение фликера

, (19)

где . По графику ощущения фликера строится функция кумулятивных вероятностей и определяются уровни фликера, а по ним – доза фликера (5).

Для периодических помех решение получается таким же образом, но в пределах длительности цикла и при ненулевой начальной ординате S(0).

Простейшим является случай гармонической помехи

(20)

с размахом колебаний d U, амплитудой и угловой частотой .

Поскольку фазы процессов не влияют на величину дозы фликера, можно условно считать, что все процессы имеют ненулевую фазу. Амплитуда реакции определяется значением АЧХ взвешивающего фильтра при .

Процесс после квадратора

содержит постоянную составляющую , а также синусоиду с амплитудой и двойной частотой.

Инерционное звено умножает постоянную составляющую на , а амплитуду синусоиды – на значение

АЧХ звена при .

Без учета фазы ощущение фликера

.

Распределение ординат процесса с гармоническими реализациями подчиняется закону арксинуса в пределах . С учетом формулы (I.29) из [9] получим функцию кумулятивных вероятностей

. (21)

Отсюда для r-го уровня фликера найдем

, (22)

чем согласно (5) решается задача определения дозы фликера.

Перейдем к случайным помехам. Из-за нелинейности квадратора задача о вероятностном распределении ощущения фликера не может быть решена аналитическим путем. В общем случае известно лишь среднее значение

, (23)

пропорциональное квадрату стандарта s Y реакции. Это значение можно использовать для оценки нижнего предела дозы фликера напряжения, который достигается в нереализуемом на практике случае постоянства ординат реакции и зрительного ощущения. При этом все уровни фликера в (5) будут одинаковыми, равными Sс. В результате получим неравенство

. (24)

Процессы с гармоническими реализациями имеют стандарт .

Для решения задачи был применен метод имитации случайных помех. Исследования показали [10], что ощущение фликера подчиняется гамма-распределению с параметрами

, ,

определяемыми средним значением и дисперсией DS ощущения фликера. Для гамма-распределения

. (25)

Во многих случаях вероятностное распределение реакции является нормальным, так как либо сама помеха подчиняется нормальному закону распределения (группа электроприемников, дуговая сталеплавильная печь) либо взвешивающий фильтр, как всякая линейная инерционная система, нормализует реакцию. Для нормального процесса с нулевым средним значением КФ квадрата реакции

, (26)

а дисперсия ощущения фликера находится по вытекающей из (14) при t = 0 формуле

, (27)

интегрирование по которой для встречающихся в практике КФ помех выполняется в конечном виде.

По обратной функции arc Er(Pr) рассчитываются уровни фликера и доза (5).

Предложенные методы расчета являются аналитически завершенными, что делает их принципиально точными, не требующими численного интегрирования. При создании соответствующих компьютерных программ использованы стандартные функции.

Примеры расчета. 1. Сопоставить реакции взвешивающего фильтра на две периодические помехи с одинаковыми размахами d U = 1 %, длительностями импульсов t1 = 0,09 c и циклов tц = 0,18 c (рис. 4,а).

На первом участке первого графика угловой коэффициент и начальная ордината , а на втором и . Подстановка этих величин в формулу (13) дает начальное значение (при t = 0) парциальной реакции

,

где , .

Согласно (12) на первом участке при парциальная реакция

.

Начальная ордината парциальной реакции на втором участке равна , поэтому формула (12) при дает

.

Рис. 4

Для второго графика на первом участке c21 = – c11 и , а на втором эти величины равны нулю. Аналогичным образом получим выражения для начальной ординаты

и парциальной реакции

на участке . На втором участке при

.

Суммируя каждое выражение по i, получим графики реакций Y1(t) и Y2(t), представленные на рис. 4, б кривыми 3 и 4. Эти реакции отличаются друг от друга и дают разные дозы фликера напряжения.

 

2. Оценить допустимость колебаний напряжения, создаваемых дуговой сталеплавильной печью в начальный период расплавления. Печь питается от сети напряжением Uн = 6 кВ с мощностью короткого замыкания . Токовая нагрузка печи представляет собой случайный процесс с КФ

, кА2.

Для перехода к потерям напряжения нагрузку необходимо умножить на коэффициент

,

а для получения КФ помехи в (%)2 КФ тока умножается на С 2. Например, дисперсия помехи

.

Расчет по формуле (27) дал КФ реакции, представленную на рис. 5. Эта КФ практически совпадает с КФ, рассчитанной только по параметрам фильтра восприятия: ошибка в дисперсии реакции составила всего 0,248 %. Это объясняется тем, что спектральная плотность помехи почти полностью находится в полосе пропускания взвешивающего фильтра.

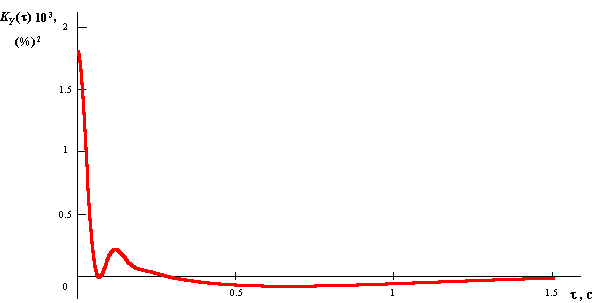
Рис. 5. Корреляционная функция реакции

Рис. 6. Функция кумулятивных вероятностей

Среднее значение ощущения фликера . Интегрирование по формуле (27) дает дисперсию . Параметры гамма-распределения:

;

.

Функция кумулятивных вероятностей, рассчитанная на компьютере, представлена на рис. 6, где стрелками показан путь определения уровня фликера для одного значения интегральной вероятности , которому соответствует уровень .

Расчет по формуле (5) дал значение кратковременной дозы , которое меньше нормы 1 для работ со зрительным напряжением, а тем более 1,38 – без зрительного напряжения. Это означает, что ЭМС не нарушается.

Полученное значение дозы на 19,6 % больше теоретического предела (24), что объясняется малым диапазоном изменения зрительного ощущения вследствие сглаживающего действия блока КС.

Выводы. 1. Для идентичности оценок ЭМС по дозе фликера напряжения, получаемых измерениями фликерметром или расчетным путем, методы измерения, расчета и нормирования должны базироваться на единой фликер-модели.

2. Расчет доз фликера целесообразно выполнять методом парциальных реакций, дающим точное аналитическое решение.

[1] ГОСТ 13109-97. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. в Украине 01.01.2000.

[2] Flickermeter. Functional and design specification. – Geneva: IEC Report. – 1986. – Publication 868. – 31 p.

[3] Mirra C., Sani G. Il fenomeno del flicker. Analisi delle sue caracteristiche. Techniche di misura e metodi di limitazione. – L’Elettrotecnica. – 1987. – Р. 805 – 822.

[4] Гутников В.С. Фильтрация измерительных сигналов. – Л.: Энергоатомиздат, 1990. – 192 с.

[5] Курінний Е.Г., Чернікова Л.В., Петросов В.А. Уніфікований метод розрахунку характеристик випадкових процесів у лінійних фільтрах моделей електромагнітної сумісності // Технічна електродинаміка / Тематичний випуск “Проблеми сучасної електротехніки -2000”, ч. 2. – 2000 – С. 20 – 23.

[6] Абу С. Сами. Методы расчета динамических показателей электромагнитной совместимости электрооборудования с периодической нагрузкой и систем электроснабжения. Автореферат диссертации на соиск. ученой cтепени канд. техн. наук. – Донецк: ДПИ, 1992. – 24 с.

[7] Курінний Е.Г., Циганкова Н.В. Імітація корельованих процесів в електричних мережах методом елементних процесів // Збірник наукових праць Донецького держ. техн. університету. Серія: “Електротехніка і енергетика”, випуск 17. – Донецьк: ДонДТУ, 2000. – С. 142 – 145.

[8] Тихонов В.И. Статистическая радиотехника. – М.: Советское радио, 1966. – 678 с.

[9] Шидловский А.К., Куренный Э.Г. Введение в статистическую динамику систем электроснабжения. – Киев: Наукова думка, 1984. – 271 с.

[10] E.G. Kourennyi, V.A. Petrosov, N.N. Pogrebnyak. Squaring and smoothing in EMC models: a statistical solution // Electromagnetic Compatibility 2000, part I, Fifteenth International Wroclaw Symposium on Electromagnetic Compatibility. – 2000. – P. 322 – 325.

Приложение. В [2] не указывается способ перехода от измерения ощущения фликера в (%)2 к безразмерным величинам. Найдем значение kи из условия, что при подаче калибровочного синусоидального сигнала амплитудой 1 % и частотой 50/17 Гц [2] доза фликера будет равна единице.

Значение АЧХ взвешивающего фильтра при калибровочной частоте w к вычислим по табл. I из [2] – как отношение допустимых размахов при резонансной и калибровочной частотах: А(w к)=0,376. При калибровочной частоте А и=0,08982 kи. Амплитуда . При найденных значениях формула (22) дает

.

По заданным кумулятивным вероятностям вычислим Р0,1 » Р1 = 0,011926 kи , Р3 = 0,01925 kи , Р10 = =0,01918 kи , Р50 = 0,01767 kи . Подстановка этих уровней в (5) дает дозу . Допустимое значение дозы будет достигнуто при

.

Отметим, что для калибровочного сигнала доза колебаний = 0,01767 (%)2 практически совпадает с допустимым значением 0,018 (%)2 из ГОСТ 13109-87 для работ со значительным зрительным напряжением.